확률
일상생활 전반에 나타나고 있는 현상들의 가능성을 수리통계적으로 표현한 것.
고대부터 도박에서 시작된 많은 연구가 실제 확률론으로 자리 잡았다.
경우의 수
= 모든 가능성을 생각해보기 위해서
순열
순서(시간)를 반영한 모든 경우의 수를 구한다.
조합
순서(시간)를 고려하지 않은 경우의 수(=패턴)
확률
전체 사건들 중 특정 사건이 발생할 가능성
P(X) = X사건이 발생할 경우의 수 / 전체 사건이 발생할 경우의 수
(X : 확률 변수)
확률분포
각 사건에 대응되는 확률의 퍼진 정도를 일반화한 것
확률분포도
확률분포를 그림으로 표현한 것으로 히스토그램의 한 종류
⇒ 과거 데이터에서 X가 어떤 값일 때의 확률값을 파악할 수 있고, 확률분포를 기반으로 미래 예측값의 가능성을 정량적으로 표현할 수 있다. 퍼센트와 같은 개념이고 전체 합은 1(100%) 이된다.
확률질량함수 / 확률밀도함수
확률분포도를 선으로 그었을때 방정식
대표적 확률 분포
이항분포
연속된 n번의 독립적 시행에서 각 시행이 확률 p를 가질 때의 이산확률분포이다.
- 확률질량함수 : 조합 x 해당 사건이 발생할 확률의 횟수 x 해당 사건이 발생하지 않을 확률의 나머지 횟수
- nCx * P^x * (1-P)^(n-x)
- 예측 기대값 : 예측되는 확률변수분포의 평균값으로, 예상되는 확률변수값을 확률 가중치로 평균한 값
- 각 (확률변수 x 발생할 확률)들의 합
- 예측 기대오차 : 예측되는 확률변수 분포의 분산값으로, 기대값으로부터 얼마나 퍼져있는지를 측정한 값
- 각 ((확률변수-기대값)^2 x 발생할 확률)들의 합
정규분포
특정 사건을 여러 번 반복했을때의 반복 확률
- 시행 횟수(n)가 증가하면 정규분포와 비슷해진다.
- 시행 횟수(n)가 증가하면 정규분포의 평균값정도로 경우의 수(n x p)가 발생한다.
- 확률밀도함수 : f(x) = ( 1 / σ√2π ) * e^( −1/2 * [ (x−μ) / σ]^2 )
- 확률변수 X가 취할 수 있는 값의 범위는 -∞ < X < ∞
- 확률 변수가 무한이기때문에 밀도라고 쓴다. (이항분포는 확률질량함수)
- 예측 기대값 : 이항분포의 기대값 의미와 똑같지만, 확률변수가 무한대의 범위이므로 적분개념표기
- 예측 기대오차 : 이항분포의 기대오차 의미와 똑같지만, 확률변수가 무한대의 범위이므로 적분개념표기
확률 분포의 종류
이산형확률분포
확률변수 X의 값이 셀 수 있는 경우의 확률 분포
확률분포도를 그리는 수학적 함수 표현식 : 확률 질량 함수, 누적 확률 질량 함수
연속형확률분포
확률변수 X의 값이 셀 수 없는 경우의 확률 분포
확률분포도를 그리는 수학적 함수 표현식 : 확률 밀도 함수, 누적 확률 밀도 함수
확률분포의 관계
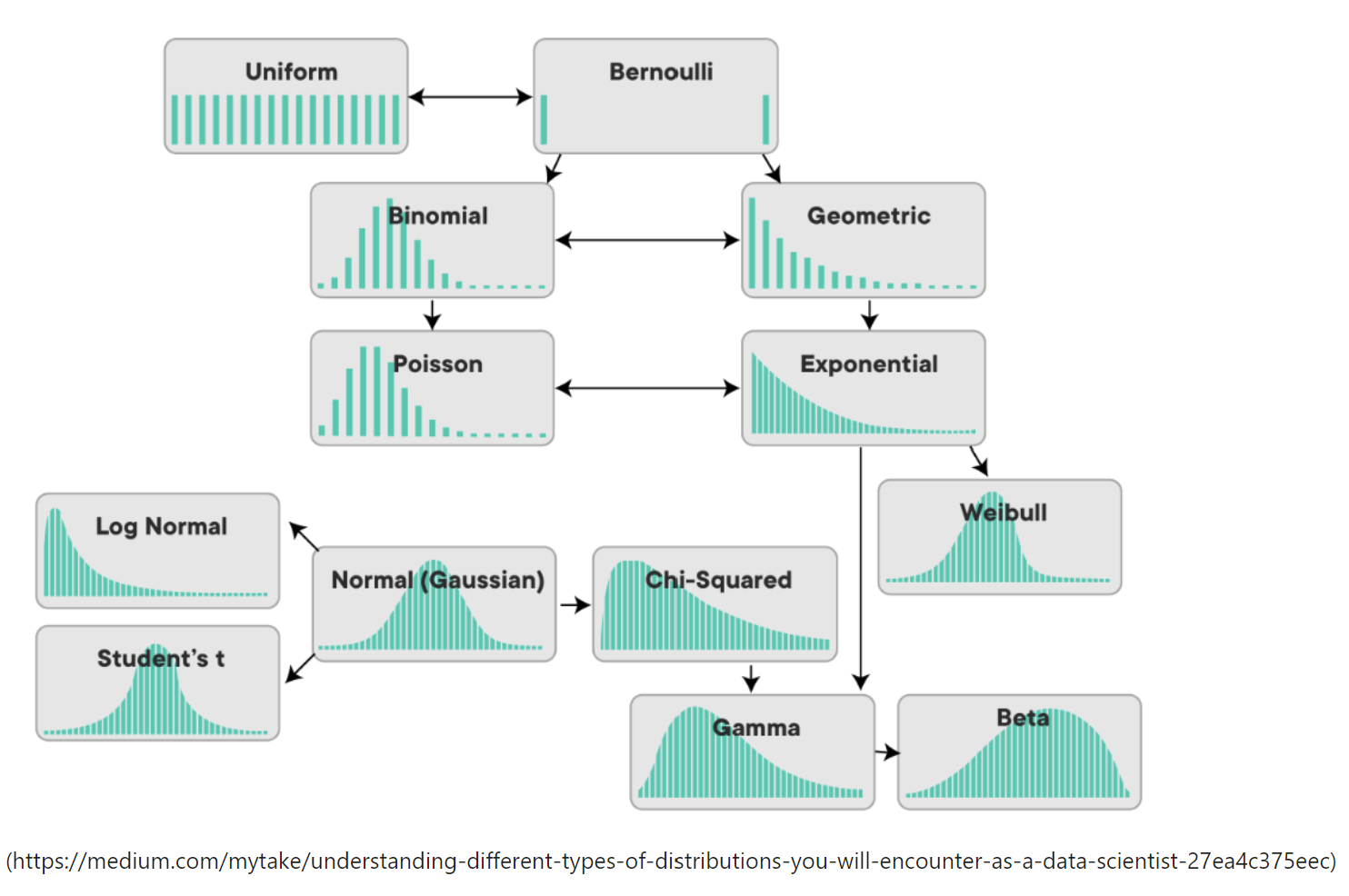

참고)
https://homepage.stat.uiowa.edu/~mbognar/
Matt Bognar
Courses Statistics for Business (STAT:1030) <!-- STAT:2020 Probability and Statistics for Eng. and Phys. Sci. STAT:3510 Biostatistics --> Introduction to Mathematical Statistics I (STAT:3100) --> Introduction to Mathematical Statistics II (STAT:3101) --> P
homepage.stat.uiowa.edu
나의 데이터는 어떤 확률분포를 따르는가
현존하는 확률분포가 어떤 것이 있는지 알고, 내 데이터와 비교(스몰데이터에서 빅데이터를 추론) 할 수 있어야 한다.
데이터 분포에 따라 향후 알고리즘에 입력될 전처리 방식이 달라질 수 있음.
⇒ 곧 모델링을 뜻한다.
데이터 분포 예측 및 검증
Kolmogorov-Smirnov Test (KS Test)
주어진 모델의 분포와 실제 데이터 분포가 얼마나 비슷한지 확률적으로 예측 및 검증.
모델과 데이터의 분포 차이가 비슷할수록 가장 큰 p-value 반환.
정리
자연현상의 대부분은 정규분포이지만 그렇지 않은 경우도 존재한다.
- 정규분포이기 위해서는 각 사건들이 영향을 주지 않는 독립적이어야하기 때문이다.
다양한 분포 종류들이 있으며, 특정되지 않을 때는 비모수 확률 분포나 베이지안 확률 분포를 사용하여 분석한다.
그럼에도 정규분포를 사용하는 이유는 대부분이 정규분포이며, 일부 변환을 통해 정규분포와 근사되도록 유도하여, 평균과 분산만 알면 확률을 쉽게 추정할 수 있기 때문이다.
* 정규분포 = 가우시안분포
모수적 모델, 비모수적 모델, 세미모수적 모델
모수 = parameter
- 모수적 모델 (통계 추론)
- 모수의 형태를 확률분포로 가정(선형회귀모델 등)
- 간단하고 빠르고 스몰데이터에 적합하지만 제한적 성능과 복잡성 한계
- 비모수적 모델 (머신러닝)
- 모수의 형태를 확률분포로 가정하지않고 주어진 데이터에서 직접 확률 계산하여 검증하는 알고리즘(KNN 등)
- 빅데이터 사용으로 유연하고 강력하지만 과적합 가능성이 있다.
- 세미모수적 모델 (딥러닝)
- 모수적 및 비모수적 모델을 상충.
- 일부에는 모수가 존재하지만 확률분포를 가정하지 않음(Neural Network 등)
'퀀트 > 금융' 카테고리의 다른 글
| 확률 | 3. 현실 확률을 다루는 방법 (빈도 확률, 베이지안 확률) (0) | 2023.02.09 |
|---|---|
| 확률 | 2. 반복되는 사건의 실제 확률 분포 (0) | 2023.02.08 |
| 금융 공학 개요 | 5. 확률, 통계 및 데이터사이언스 (0) | 2023.02.06 |
| 금융 공학 개요 | 4. 금융 공학 모델링 및 데이터사이언스 (0) | 2023.02.04 |
| 금융 공학 개요 | 3. 금융 공학의 역사 (0) | 2023.02.03 |